<통계량의 2가지 종류>
산포도 : 자료가 흩어진 정도를 나타내는 값
* 자료값이 대표값 근처에 모일수록 산포도는 작아진다.
집중화 경향 : 자료 값이 어느 위치에 집중되어 있는지 나타내는 척도
01. 이산확률분포
떨어져있는 확률변수 x에 대한 확률분포
ex.주사위를 던져 나올 수 있는 눈(=확률변수 x) = 1,2,3,4,5,6 = 떨어져 있고, 셀 수 있으므로 이산확률분포이다.
| 1 | 2 | 3 | 4 | 5 | 6 | 합 | |
| p(x) | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1 |
* p(x) : x라는 변수가 나올 확률
평균 : E(x)
E(x) = Σ x * p(x)
= 1*⅙ + 2*⅙ + 3*⅙ + 4*⅙ + 5*⅙ + 6*⅙
= 1+2+3+4+5+6/6
= 21/6
= 3.5
분산 : V(x)
V(x) = E(x²) - (E(x))²
= (1*⅙ + 4*⅙ + 9*⅙ + 16*⅙ + 25*⅙ + 36*⅙) - (7/2)²
= V
표준편차 : σ(x)
σ(x) = √V
02. 이항분포 B(n,p)
이산확률분포의 한 종류
어떤 일을 1번 시행할 때 일어날 확률(되는확률) p, 안 되는 확률 q, n번 시행했을 때 일어난 횟수를 확률변수 x라 한다.
매 시행마다 일어날 확률이 반드시 일정해야한다.
ex. 동전을 던졌을 때, 주사위를 던졌을 때
이항분포에서 확률을 구하는 공식
p(x=r)= nCr * p^r * q^n-r
[예제] 동전 2개를 5번 던진다. 이 때 둘 다 앞면이 나올 횟수를 확률변수x라고 하자.
p=1/4, q=3/4, n=5, x=0,1,2,3,4,5
B(5, 1/4)
평균E(x)
= np
= 5/4
분산V(x)
= npq
= 5 * 1/4 * 3/4
= 15/16
표준편차σ(x)
= √npq
= √15/4
03. 연속확률분포와 확률밀도함수
연속확률분포? 확률변수 x가 연속해있다. ex. 시간, 몸무게, 키
그래프가 여러가지 모양으로 나타날 수 있다.
확률은 구간의 넓이이다.
시작~끝의 확률은 반드시 1이다.
04. 정규분포 N(m,σ²) =N(평균,표준편차²)
확률밀도함수의 한 종류.
최고점이 곧 평균(0)이다.
평균을 중심으로 좌우대칭이다.
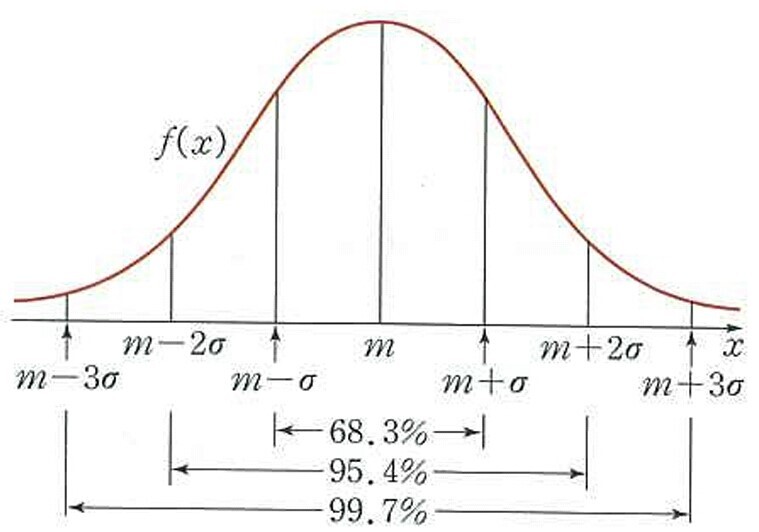
05. 이항분포 -> 정규분포
B(n,p) -> N(m,σ²)
이항분포의 n이 30보다 크면 정규분포가 될 수 있다.
ex. 이항분포 B(100, 1/4)를
E(x) = 100 * 1/4 = 25
V(x) = 100 * 1/4 * 3/4 = 25 *3/4 = 75/4
σ(x) = √75/4 = 5√3/2
정규분포로 바꾸기
N(25, (5√3/2))²
06. n개를 임의추출(=표본을 뽑는다)
변수 x
E(x) = m
v(x) = σ²
σ(x) = σ
⬇임의추출 n개⬇
변수 x̄ (표본평균)
E(x̄) = m
v(x̄) = σ²/n
σ(x̄) = σ/√n
07. 통계적 추정 / 모평균의 추정
x̄ - k * σ/√n ≤ m ≤ x̄ + k * σ/√n : 신뢰구간
x̄ : 표본평균
σ : 모 표준편차 (n ≥ 30이면 varσ)
k : 신뢰도 상수 95% (k=1.96) or 99% (k=2.58)
분산과 표준편차
분산 : 산포도에 속하는 통계량. 자료가 평균을 중심으로 얼마나 퍼져 있는지 나타내는 대표적인 수치. 평균과 각 값의 차이의 제곱에 대한 평균.
표준편차 : 산포도에 속하는 통계량. 자료가 평균을 중심으로 얼마나 퍼져 있는지 나타내는 대표적인 수치. 분산에 제곱은을 적용해 계산.
평균 = 자료 값의 총 합/자료의 개수
편차 = 자료의 값 - 평균
* 편차의 성질
편차의 합은 항상 0
변량이 평균보다 크면 그 편차는 양수이고, 변량이 평균보다 작으면 그 편차는 음수
편차의 절대값이 클수록 변량은 평균에서 멀고, 편차의 절대값이 작을수록 변량은 평균과 가깝다
분산 = (편차)^2의 합/자료의 개수
표준편차 = √분산
* 표준편차 구하는 순서 : 변량의 평균 > 편차 > 분산 > 표준편차
* 분산과 표준편차가 작을수록 자료값들이 평균에 모여있다는 것을 의미한다 (=자료의 분포 상태가 고르다)
* 표준편차는 주어진 자료와 같은 단위를 사용하고, 분산은 단위를 사용하지 않는다
[참고영상] https://youtu.be/CQA7cdxozHY
'개인공부 > R' 카테고리의 다른 글
| 21. R 통계기본개념2 (통계분석모델) (0) | 2021.10.05 |
|---|---|
| 19. R EDA, 데이터전처리 연습문제 (0) | 2021.10.03 |
| 15. R ggplot (0) | 2021.09.29 |
| 14. R기초연습문제 (0) | 2021.09.28 |
| 13. R정리 (데이터 정제, 그래프 만들기) (0) | 2021.09.27 |