비지도학습(unSupervised Learning) 절차
데이터셋 > 알고리즘 적용 > 패턴분석 > 규칙발견 > 모델 생성 > 평가 > YES : 미래예측 / NO : 처음부터 다시
01. 군집 분석 개요
군집 분석?
대상 객체를 유사하거나 서로 관련 있는 항목 끼리 묶어서 몇 개의 집단으로 그룹화하는 것
* 분류분석과 가장 큰 차이점 : 정답이 없는 것들을 최대한 비슷한 것 끼리 묶어준다. (데이터 안에 정답이 있으면 묶어주는 것이 분류분석)
군집분석 특징
전체적인 데이터 구조를 파악하는데 이용
종속변수(y변수)가 없는 비지도학습(데이터 마이닝) 기법
관측대상 간 유사성을 기초로 비슷한 것 끼리 그룹화(Clustering)
유사성 = 유클리드 거리식 이용
석결과에 대한 가설 검정 없음 (타당성 검증 방법 없음)
척도 : 등간, 비율척도(연속적인 양)
계층적 군집분석(탐색적) / 비계층적 군집분석(확인적)
주요 알고리즘 : hierarchical, k-means
유클리드 거리계산식
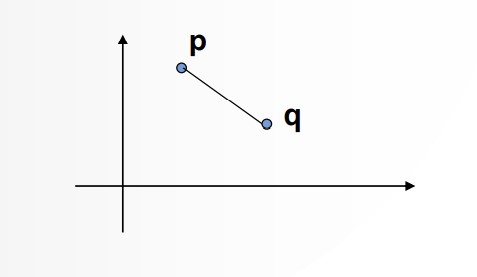
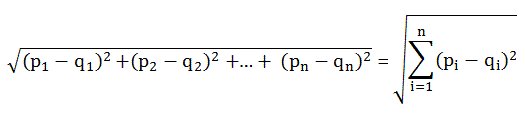
관측대상 간 유사성을 기초로 비슷한 것 끼리 그룹화(Clustering)
유사성 = 유클리드 거리 이용
* 관측대상 p와 q의 값의 차가 작으면, 두 관측 대상은 유사하다고 정의하는 식
계층적 군집분석 군집화 방법
* 데이터분석 시험문제에 자주 출제
| 최단연결법 | 두 군집 간의 가장 가까운 관측치 간 연결 |
| 최장연결법 | 두 군집 간의 가장 먼 거리의 관측치 간 연결 |
| 평균연결법 | 두 군집 간의 가능한 모든 거리의 평균 기준 연결 |
| 중심연결법 | 각 군집의 중심(centroid) 간 거리 기준 연결 |
| 와드연결법 | 두 군집이 합쳐질 때 오차제곱합(ESS)의 증분으로 연결 * ESS의 증분에 따라서 두 군집의 거리 측정으로 연결, 중심연결법과 유사함 |
* 유클리드 거리계산식 이용 : 최단,최장,평균,중심 연결법

최단연결법 (단일기준결합방식)
각 군집에서 중심으로부터 거리가 가까운 것(2,3,6) 1개씩 비교하여 가장 가까운 것 끼리 군집화
최장연결법 (완전기준결합방식) : 기본으로 사용. 각 군집에서 중심으로부터 가장 먼 대상(1,4,5) 끼리 비교하여 가장 가까운 것 끼리 군집화
평균연결법 (평균기준결합방식) : 한 군집 안에 속해 있는 모든 대상과 다른 군집에 속해있는 모든 대상의 쌍 집합에 대한 거리를 평균 계산하여 가장 가까운 것 끼리 군집화 (1 -> 5,6 평균, 2 -> 5, 6 평균)
[실습] 그룹화를 통한 예측(그룹 특성 차이 분석-고객집단 이해)
1. 유클리드 거리 (p-q)^2
유클리드 거리(Euclidean distance)는 두 점 사이의 거리를 계산하는
방법으로 이 거리를 이용하여 유클리드 공간을 정의한다.
(1) matrix 생성
x <- matrix(1:9, nrow=3, by=T)
x [,1] [,2] [,3]
[1,] 1 2 3 -> p
[2,] 4 5 6 -> q
[3,] 7 8 9
3 3 3 -> p+p+p = 27 -> √27
sqrt(27) #1,2번 행에 대한 거리 : 5.196152
sqrt(36+36+36) #1,3번 행에 대한 거리 : 10.3923
(2) matrix 대상 유클리드 거리 생성 함수
형식) dist(x, method="euclidean") -> x : numeric matrix, data frame
dist <- dist(x, method="euclidean") #x행렬/매트릭스를 대상으로 유클리드 거리 계산. (method 생략가능)
dist 1 2
2 5.196152
3 10.392305 5.196152
1행(p) vs 2행(q)
sqrt(sum((x[1, ] - x[2,])^2)) #5.196152
1행(p) vs 3행(q)
sqrt(sum((x[1, ] - x[3,])^2)) #10.3923 (통상적으로 2배 차이)
* 유클리드 거리 계산식 활용분야
1. 분류모델 : kNN
2. 군집모델 : 계층적 / 비계층적
3. 추천모델 : 유사도 계산
4. 좌표 거리계산 : 위도와 경도
2. 계층적 군집분석(탐색적 분석)
계층적 군집분석(Hierarchical Clustering) 트리 구조에서 사용되는 대표 방법 ex.회사 조직도
거리가 가장 가까운 대상부터 결합하여 나무모양의 계층구조를 상향식(Bottom-up)으로 만들어가면서 군집을 형성
(1) 군집분석(Clustering)분석을 위한 패키지 설치
install.packages("cluster") #hclust() : 계층적 클러스터 함수 제공
library(cluster) #일반적으로 3~10개 그룹핑이 적정
(2) 데이터 셋 생성
r <- runif(15, min = 1, max = 50) #1이상 50이하의 난수 15개 생성성
x <- matrix(r, nrow=5, by=T) #[5,3]
x
(3) matrix 대상 유클리드 거리 생성 함수
dist <- dist(x, method="euclidean") # method 생략가능
dist 1 2 3 4
2 4.114234
3 35.401012 31.626887
4 37.947768 34.295621 18.655243
5 25.066933 27.803212 49.155692 56.803235
* 5개의 관측치 중 1,2가 거리가 가장 가깝다 (=유사성이 높다)
* 정말일까?
[,1] [,2] [,3]
[1,] 34.185929 17.089664 35.37096
[2,] 30.240518 18.241765 35.55348 -> 1,2행의 값들이 서로 유사함을 발견할 수 있다
[3,] 1.831156 25.291404 23.57555
[4,] 5.630017 41.771791 31.44851
[5,] 45.757080 4.141226 17.29342
(4) 유클리드 거리 matrix를 이용한 클러스터링
hc = hclust(dist, method="complete") #완전결합기준
군집 방법(Cluster method)
method = "complete" : 완전결합기준(최대거리 이용) <- default(생략 시)
method = "single" : 단순결합기준(최소거리 이용)
method = "average" : 평균결합기준(평균거리 이용)
help(hclust)
plot(hc) # 클러스터 플로팅(Dendrogram) -> 1과2 군집(클러스터) 형성
[실습] 중1학년 신체검사 결과 군집분석
단계1 : 데이터셋 가져오기
body <- read.csv("c:/ITWILL/2_Rwork/data/bodycheck.csv")
names(body)
단계2 : 거리계산
idist <- dist(body)
idist
단계3 : 계층적 군집분석
hc <- hclust(idist)
plot(hc, hang=-1) # 음수값 제외
3개 그룹 선정, 선 색 지정
rect.hclust(hc, k=3, border="red") # 3개 그룹 선정, 선 색 지정
단계4 : 각 그룹별 서브셋 만들기 (소량의 데이터)
g1<- body[c(10,4,8,1,15), ]
g2<- body[c(11,3,5,6,14), ]
g3<- body[c(2,9,13,7,12), ]
단계5 : 군집별 특성분석
summary(g1) 번호 악력 신장 체중 안경유무
Mean : 7.6 Mean :25.6 Mean :149.8 Mean :36.6 Mean :1
[해석] 왜소한 집단
summary(g2)
Mean : 7.8 Mean :33.8 Mean :161.2 Mean :48.8 Mean :1.4
[해석] 중간 정도의 집단
summary(g3)Mean : 8.6 Mean :40.6 Mean :158.8 Mean :56.8 Mean :2
[해석] 몸집이 큰 집단

cutree()함수
대량 dataset 그룹별 서브셋 생성
형식) cutree(object, k=군집수)
g_num = cutree(hc, k=3) #1~3으로 각각의 관측치를 반환
g_num # 1 2 3 1 3 3 2 1 2 1 3 2 2 3 1
칼럼추가
body$cluster = g_num
head(body)
번호 악력 신장 체중 안경유무 cluster
1 1 28 146 34 1 1 -> 1번 군집에 속한다
2 2 46 169 57 2 2
3 3 39 160 48 2 3
4 4 25 156 38 1 1
5 5 34 161 47 1 3
6 6 29 168 50 1 3
g1 = subset(body, cluster==1)
g1$'번호'
g2 = subset(body, cluster==2)
g2$'번호'
g3 = subset(body, cluster==3)
g3$'번호'summary(g1) #g1==g1
summary(g2) #g2==g2
summary(g3) #g3==g3 이전의 단계 4번과 같은 값 출력
'데이터분석가 과정 > R' 카테고리의 다른 글
| DAY27. R 연관분석 (0) | 2021.10.22 |
|---|---|
| DAY26. R 군집분석(2) (0) | 2021.10.21 |
| DAY24. R 분류분석 (0) | 2021.10.19 |
| DAY23. R 로지스틱회귀분석 (0) | 2021.10.18 |
| DAY22. R 기계학습이론, 선형회귀분석 (0) | 2021.10.15 |