AI 실무 응용 과정
[응용교육과정] 머신러닝 시작하기 (2) 지도학습 - 회귀
회귀 개념 알아보기
[가정] 아이스크림 가게 운영자일 때, 예상되는 실제 판매량만큼만의 주문량을 원한다. 이 때 만약 평균 기온을 이용해 판매량을 예상할 수 있다면?
[문제 정의]
데이터 : 과거 평균 기온(X)과 그에 따른 아이스크림 판매량(y)
가정 : 평균 기온과 판매량은 선형적인 관계를 가지고 있음 * 선형 관계 : 같은 증감 경향성을 보이는 관계
목표 : 평균 기온에 다른 아이스크림 판매량 예측하기
해결방안 : 예측대상이 있고, 그에 대한 feature label이 있으므로 지도학습 -> 예측해야할 y데이터가 수치형 값이므로 회귀 분석 알고리즘
회귀 분석이란?
label이 수치형일 때, 데이터를 가장 잘 설명하는 모델을 찾아 입력값에 따른 미래 결과값을 예측하는 알고리즘
주어진 데이터 X : 평균기온, y : 아이스크림 판매량
가정 : Y = β0 + β1X (직선모델)
목표 : 적절한 β0, β1값(데이터를 가장 잘 설명하는 모델)을 찾자
적절한 β0, β1값 찾기
완벽한 예측은 불가능하므로 최대한 잘 근사해야한다.
각 데이터의 실제 값과 모델이 예측하는 값의 차이를 최소한으로 하는 선을 찾자.
단순 선형 회귀 모델을 학습하며 차이를 최소한으로 하는 선을 찾는 방법을 알아보자.
단순 선형 회귀
단순선형회귀란?
데이터를 설명하는 모델을 직선 형태로 가정한 것
Y = β0 + β1X
직선을 구성하는 β0(y절편)와 β1(기울기)를 구해야 함
데이터를 잘 설명한다는 것은?
실제 정답과 내가 예측한 값과의 차이가 작을수록 좋지 않을까?

-> 왼쪽 그래프의 차이가 오른쪽에 비해 적어 보인다.
실제 값과 예측 값의 차이를 구해보자.

실제 값과 예측 값의 차이의 합으로 비교하기에는 예외가 있다.

[해석] 합계가 둘 다 0이지만, 우측의 그래프가 100%를 설명하고 있다. 실제값과 예측값의 합은 좋은 방법이 아니다.
실제 값과 예측 값의 차이의 제곱의 합으로 비교하자.

Loss함수
실제 값과 예측 값 차이의 제곱의 합을 Loss함수로 정의한다. -> Loss함수가 작을수록 좋은 모델
Loss함수 줄이기
Loss함수에서 주어진 값은 입력 값과 실제 값이다.
β0(y절편)와 β1(기울기) 값을 조절하여 Loss함수의 크기를 작게 만든다 -> 거의 모든 직선을 그릴 수 있다!
기울기 값이 커지면 직선이 위쪽으로 솟고, 기울기 값이 작아지면 직선이 아래로 내려간다 -> 각도 조절
절편이 커지면 y축 위쪽에서 시작하는 직선, 절편이 작아지면 y축 아래에서 시작하는 직선
Loss값을 구해서 그 직선이 얼마나 좋은 직선인지 판단할 수 있는 근거가 된다
Loss함수의 크기를 작게 하는 β0(y절편)와 β1(기울기)를 찾는 방법

1) Gradient descent (경사 하강법)
2) Normal equation (least squares)
3) Brute force search
4) ...
경사하강법
Loss함수 값이 제일 작게 하는 절편, 기울기를 β0*, β1*이라고 하자.
경사 하강법은 계산 한번으로 β0*, β1*를 구하는 것이 아니라, 초기값에서 점진적으로 구하는 방식이다.
* 초기값 : 임의의 β0*, β1*값
β0, β1값을 Loss함수 값이 작아지게 계속 update하는 방법

1) β0, β1값을 랜덤하게 초기화
2) 현재 β0, β1값으로 Loss값 계산
3) 현재 β0, β1값을 어떻게 변화시켜야 Loss값을 줄일 수 있는지 알 수 있는 Gradient값 계산
* Gradient값 : Loss값을 줄일 수 있게 하는지에 대한 힌트, 이미지에서 하강하는 방향
4) Gredient값을 활용하여 β0, β1값 업데이트
5) Loss값의 차이가 거의 없어질 때까지 2~4번 과정을 반복 (Loss값과 차이가 줄면, Gradient값도 작아짐)
단순 선형 회귀 과정
1) 데이터 전처리 -> X, Y값
2) 단순 선형 회귀 모델 학습 -> 경사하강법
3) 새로운 데이터에 대한 예측 -> 최종적인 직선 구하기 (Loss값이 제일 적음)
단순 선형 회귀 특징
가장 기초적, 여전히 많이 사용되는 알고리즘
입력값이 1개인 경우에만 적용 가능
입력값과 결과값의 관계를 알아보는데 용이
입력값이 결과값에 얼마나 영향을 미치는지 알 수 있음
두 변수 간의 관계를 직관적으로 해석하고자 하는 경우 활용
[연습문제] 단순 선형 회귀 분석하기 - 데이터 전 처리
주어진 데이터를 sklearn에서 불러 올 선형 모델에 적용하기 위해서는 전 처리가 필요합니다.
이번 실습에서는 sklearn에서 제공하는 LinearRegression을 사용하기 위한 데이터 전 처리를 수행해보겠습니다.
LinearRegression 모델의 입력값으로는 Pandas의 DataFrame의 feature (X) 데이터와 Series 형태의 label (Y) 데이터를 입력 받을 수 있습니다.
X, Y의 샘플의 개수는 같아야 합니다.
1. X 데이터를 column 명이 X인 DataFrame으로 변환하고 train_X에 저장합니다.
2. 리스트 Y를 Series 형식으로 변환하여 train_Y에 저장합니다.
import matplotlib as mpl
mpl.use("Agg")
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression
import elice_utils
eu = elice_utils.EliceUtils()
X = [8.70153760, 3.90825773, 1.89362433, 3.28730045, 7.39333004, 2.98984649, 2.25757240, 9.84450732, 9.94589513, 5.48321616]
Y = [5.64413093, 3.75876583, 3.87233310, 4.40990425, 6.43845020, 4.02827829, 2.26105955, 7.15768995, 6.29097441, 5.19692852]
#1. X의 형태를 변환하여 train_X에 저장합니다.
train_X = pd.DataFrame(X, columns=['X'])
#2. Y의 형태를 변환하여 train_Y에 저장합니다.
train_Y = pd.Series(Y)
#변환된 데이터를 출력합니다.
print('전 처리한 X 데이터: \n {}'.format(train_X))
print('전 처리한 X 데이터 shape: {}\n'.format(train_X.shape))
print('전 처리한 Y 데이터: \n {}'.format(train_Y))
print('전 처리한 Y 데이터 shape: {}'.format(train_Y.shape))
[연습문제2] 단순 선형 회귀 분석하기 - 학습하기
기계학습 라이브러리 scikit-learn 을 사용하면 Loss 함수를 최소값으로 만드는 β0, β1을 쉽게 구할 수 있습니다.
[연습문제1]에서 전 처리한 데이터를 LinearRegression 모델에 입력하여 학습을 수행해봅시다.
import matplotlib as mpl
mpl.use("Agg")
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression
import elice_utils
eu = elice_utils.EliceUtils()
X = [8.70153760, 3.90825773, 1.89362433, 3.28730045, 7.39333004, 2.98984649, 2.25757240, 9.84450732, 9.94589513, 5.48321616]
Y = [5.64413093, 3.75876583, 3.87233310, 4.40990425, 6.43845020, 4.02827829, 2.26105955, 7.15768995, 6.29097441, 5.19692852]
train_X = pd.DataFrame(X, columns=['X'])
train_Y = pd.Series(Y)
#1. 모델을 초기화 합니다.
lrmodel = LinearRegression()
#2. train_X, train_Y 데이터를 학습합니다.
lrmodel.fit(train_X, train_Y)
#학습한 결과를 시각화하는 코드입니다.
plt.scatter(X, Y)
plt.plot([0, 10], [lrmodel.intercept_, 10 * lrmodel.coef_[0] + lrmodel.intercept_], c='r')
plt.xlim(0, 10)
plt.ylim(0, 10)
plt.title('Training Result')
plt.savefig("test.png")
eu.send_image("test.png")
[연습문제3] 단순 선형 회귀 분석하기 - 예측하기
[실습2]의 학습한 모델을 바탕으로 예측 값을 구해봅시다.
LinearRegression을 사용하여 예측을 해야한다면 predict 함수를 사용합니다.
1. lrmodel을 학습하고 train_X의 예측값을 구하여 pred_X에 저장합니다.
import matplotlib as mpl
mpl.use("Agg")
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
from sklearn.linear_model import LinearRegression
import elice_utils
eu = elice_utils.EliceUtils()
X = [8.70153760, 3.90825773, 1.89362433, 3.28730045, 7.39333004, 2.98984649, 2.25757240, 9.84450732, 9.94589513, 5.48321616]
Y = [5.64413093, 3.75876583, 3.87233310, 4.40990425, 6.43845020, 4.02827829, 2.26105955, 7.15768995, 6.29097441, 5.19692852]
train_X = pd.DataFrame(X, columns=['X'])
train_Y = pd.Series(Y)
#모델을 트레이닝합니다.
lrmodel = LinearRegression()
lrmodel.fit(train_X, train_Y)
#1. train_X에 대해서 예측합니다.
pred_X = lrmodel.predict(train_X)
print('train_X에 대한 예측값 : \n{}\n'.format(pred_X))
print('실제값 : \n{}'.format(train_Y))
다중 선형 회귀
[가정] 만약, 입력값 X에 강수량이 추가된다면?
즉, 평균 기온과 평균 강수량에 따른 아이스크림 판매량을 에측하고자 할 때

여러 개의 입력값(X)으로 결과값(Y)을 예측하고자 하는 경우 -> 다중 선형 회귀
다중 선형 회귀 모델 이해하기

입력값 X가 여러 개(2개 이상)인 경우 활용할 수 있는 회귀 알고리즘
각 개별 Xi에 해당하는 최적의 βi를 찾아야 한다.
선형 관계를 가정한다.
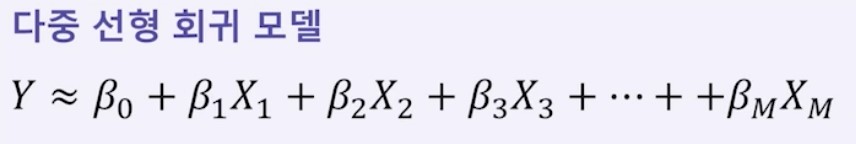
다중 선형 회귀 모델의 Loss함수
단순 선형 회귀와 마찬가지로 Loss함수는 입력값과 실제값 차이의 제곱의 합으로 정의한다.
마찬가지로 β0, β1, β2...βm 값을 조절하여 Loss함수의 크기를 작게 한다.
평균 기온과 평균 강수량으로 아이스크림 판매량 예측 예시

543.94/4 = Loss값은 약 133
다중 선형 회귀 모델의 경사 하강법
β0, β1, β2...βm 값을 Loss함수 값이 작아지게 계속 업데이트 하는 방법
1) β0, β1, β2...βm 값을 랜덤하게 초기화
2) 현재 β0, β1, β2...βm 값으로 Loss값 계산
3) 현재 β0, β1, β2...βm 값을 어떻게 변화시켜야 Loss값을 줄일 수 있는지 알 수 있는 Gradient값 계산
* Gradient값 : Loss값을 줄일 수 있게 하는지에 대한 힌트
4) Gredient값을 활용하여 β0, β1, β2...βm 값 업데이트
5) Loss값의 차이가 거의 없어질 때까지 2~4번 과정을 반복 (Loss값과 차이가 줄면, Gradient값도 작아짐)
평균 기온과 평균 강수량으로 아이스크림 판매량 예측 예시

42.89/4 = Loss값은 약 10
이전의 133에서 Loss값이 현저히 줄었음을 알 수 있다.
다중 선형 회귀 특징
여러 개의 입력값과 결과값 간의 관계 확인 가능
어떤 입력값이 결과값에 어떠한 영향을 미치는지 알 수 있음
여러 개의 입력값 사이 간의 상관관계가 높을 경우 결과에 대한 신뢰성을 잃을 가능성이 있음
* 상관관계 : 두 가지 것의 한쪽이 변화하면 다른 한쪽도 따라서 변화하는 관계
* 만약 X1과 X2의 상관관계가 높다면? β는 각각의 X에 대해 얼마나 영향을 미치는지를 알고 싶어 상정한 변수인데, X1이 커질 때 X2도 커지면 서로의 β에 영향을 미치게 되고, 가정을 벗어난다 (신뢰성을 잃는다)
[연습문제4] 다중 회귀 분석하기 - 데이터 전 처리
FB, TV, Newspaper 광고에 대한 비용 대비 Sales 데이터가 주어졌을 때, 이를 다중 회귀 분석으로 분석해봅시다.
데이터를 전 처리 하기 위해서 3개의 변수를 갖는 feature 데이터와 Sales 변수를 label 데이터로 분리하고 학습용, 평가용 데이터로 나눠봅시다.
1. DataFrame으로 읽어 온 df에서 Sales 변수는 label 데이터로 Y에 저장하고 나머진 X에 저장합니다.
2/ train_test_split를 사용하여 X, Y를 학습용:평가용=8:2학습용 : 평가용 = 8:2학습용:평가용=8:2 비율로 분리합니다. (random_state=42는 고정합니다.)
import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
from sklearn.model_selection import train_test_split
df = pd.read_csv("data/Advertising.csv")
print('원본 데이터 샘플 :')
print(df.head(),'\n')
#입력 변수로 사용하지 않는 Unnamed: 0 변수 데이터를 삭제합니다
df = df.drop(columns=['Unnamed: 0'])
#1. Sales 변수는 label 데이터로 Y에 저장하고 나머진 X에 저장합니다.
X = df.drop(columns=['Sales'])
Y = df['Sales']
#2. 학습용 평가용 데이터로 분리합니다.
train_X, test_X, train_Y, test_Y = train_test_split(X, Y, test_size=0.2, random_state=42)
#전 처리한 데이터를 출력합니다
print('train_X : ')
print(train_X.head(),'\n')
print('train_Y : ')
print(train_Y.head(),'\n')
print('test_X : ')
print(test_X.head(),'\n')
print('test_Y : ')
print(test_Y.head())
[연습문제5] 다중 회귀 분석하기 - 학습하기
[실습4]에서 전 처리한 데이터를 바탕으로 다중 선형 회귀 모델을 적용해보겠습니다.
다중 선형 회귀 또한 선형 회귀 모델과 같은 방식으로 LinearRegression을 사용할 수 있습니다.
이번 실습에서는 학습용 데이터를 다중 선형 회귀 모델을 사용하여 학습하고, 학습된 파라미터를 출력해봅시다.
LinearRegression의 beta와 같은 파라미터들은 아래 코드와 같이 구할 수 있습니다.
lrmodel = LinearRegression()
lrmodel.intercept_
lrmodel.coef_[i]
1. 다중 선형 회귀 모델 LinearRegression을 불러와 lrmodel에 초기화하고 fit을 사용하여 train_X, train_Y데이터를 학습합니다.
2. 학습된 모델 lrmodel에서 beta_0, beta_1, beta_2, beta_3에 해당하는 파라미터를 불러와 저장합니다.
import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
from sklearn.model_selection import train_test_split
#데이터를 읽고 전 처리합니다
df = pd.read_csv("data/Advertising.csv")
df = df.drop(columns=['Unnamed: 0'])
X = df.drop(columns=['Sales'])
Y = df['Sales']
train_X, test_X, train_Y, test_Y = train_test_split(X, Y, test_size=0.2, random_state=42)
#1. 다중 선형 회귀 모델을 초기화 하고 학습합니다
lrmodel = LinearRegression()
lrmodel.fit(train_X, train_Y)
#2. 학습된 파라미터 값을 불러옵니다
beta_0 = lrmodel.intercept_ # y절편 (기본 판매량)
beta_1 = lrmodel.coef_[0] # 1번째 변수에 대한 계수 (페이스북)
beta_2 = lrmodel.coef_[1] # 2번째 변수에 대한 계수 (TV)
beta_3 = lrmodel.coef_[2] # 3번째 변수에 대한 계수 (신문)
print("beta_0: %f" % beta_0)
print("beta_1: %f" % beta_1)
print("beta_2: %f" % beta_2)
print("beta_3: %f" % beta_3)
[연습문제6] 다중 회귀 분석하기 - 예측하기
[실습5]에서 학습한 다중 선형 회귀 모델을 바탕으로 이번엔 새로운 광고 비용에 따른 Sales 값을 예측해봅시다.
LinearRegression을 사용하여 예측을 해야한다면 아래와 같이 predict 함수를 사용합니다.
pred_X = lrmodel.predict(X)
1. lrmodel을 학습하고 test_X의 예측값을 구하여 pred_X에 저장합니다.
2. lrmodel을 학습하고 주어진 데이터 df1의 예측값을 구하여 pred_df1에 저장합니다.
import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
from sklearn.model_selection import train_test_split
#데이터를 읽고 전 처리합니다
df = pd.read_csv("data/Advertising.csv")
df = df.drop(columns=['Unnamed: 0'])
X = df.drop(columns=['Sales'])
Y = df['Sales']
train_X, test_X, train_Y, test_Y = train_test_split(X, Y, test_size=0.2, random_state=42)
#다중 선형 회귀 모델을 초기화 하고 학습합니다
lrmodel = LinearRegression()
lrmodel.fit(train_X, train_Y)
print('test_X : ')
print(test_X)
#1. test_X에 대해서 예측합니다.
pred_X = lrmodel.predict(test_X)
print('test_X에 대한 예측값 : \n{}\n'.format(pred_X))
#새로운 데이터 df1을 정의합니다
df1 = pd.DataFrame(np.array([[0, 0, 0], [1, 0, 0], [0, 1, 0], [0, 0, 1], [1, 1, 1]]), columns=['FB', 'TV', 'Newspaper'])
print('df1 : ')
print(df1)
#2. df1에 대해서 예측합니다.
pred_df1 = lrmodel.predict(df1)
print('df1에 대한 예측값 : \n{}'.format(pred_df1))
회귀 평가 지표
어떤 모델이 좋은 모델인지를 어떻게 평가할 수 있을까?
목표를 얼마나 잘 달성했는지 정도를 평가해야 한다.
실제 값과 모델이 예측하는 값의 차이에 기반한 평가 방법을 사용한다. ex) RSS, MSE, MAE, MATE, R^2
RSS 단순 오차
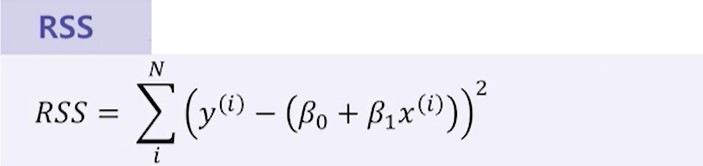
1. 실제 값과 예측 값의 단순 오차 제곱 합
2. 값이 작을수록 모델의 성능이 높음
3. 전체 데이터에 대한 실제 값과 예측하는 값의 오차 제곱의 총합
RSS 특징
가장 간단한 평가 방법으로 직관적인 해석이 가능
그러나 오차를 그대로 이용하므로 입력 값의 크기에 의존적임 (데이터의 범위 자체가 작으면 RSS도 작고, 범위가 크면 RSS도 크다)
절대적인 값과 비교가 불가능
MSE, MAE (절대적인 크기에 의존한 지표)

1. MSE(Mean Squared Error)
평균 제곱 오차, RSS에서 데이터 수 만큼 나눈 값.
작을수록 모델의 성능이 높다고 평가할 수 있다.
* MSE는 지표, Loss는 모델에서 줄여야 하는 값

2. MAE(Mean Absolute Error)
평균 절대값 오차, 실제 값과 예측 값의 오차의 절대값의 평균
작을수록 모델의 성능이 높다고 평가할 수 있다.
MSE, MAE 특징
MSE : 이상치(Outlier) 즉, 데이터들 중 크게 떨어진 값에 민감하다
MAE : 변동성이 큰 지표와 낮은 지표를 같이 예측할 때 유용하다
가장 간단한 평가 방법들로 직관적 해석이 가능
그러나 평균을 그대로 이용하므로 입력 값의 크기에 의존적
절대적인 값과 비교 불가능
R^2 결정 계수

회귀 모델의 설명력을 표현하는 지표
1에 가까울수록 높은 성능의 모델이라고 해석할 수 있다

TSS는 데이터 평균 값과 실제 값 차이의 제곱
RSS는 예측에 의한 회귀선을 긋고, 그 회귀선과 실제 값과의 차이
* TSS > RSS. RSS를 0에 가까운 값을 도출해낼수록, R^2의 값도 1에 가까워진다 (좋은 예측)
0에 가까우면 좋지 못한 예측, 음수가 도출되면 완전 헛다리 모델
R^2 특징
오차가 없을 수록 1에 가까운 값을 갖음
값이 0인 경우, 데이터의 평균 값을 출력하는 직선 모델을 의미
음수 값이 나온 경우, 평균 값 예측보다 성능이 좋지 않음
[연습문제7] 회귀 알고리즘 평가 지표 - MSE, MAE
[실습6] 에 이어서 Sales 예측 모델의 성능을 평가하기 위해서 다양한 회귀 알고리즘 평가 지표를 사용하여 비교해보겠습니다.
MSE와 MAE는 sklearn 라이브러리 함수를 통하여 쉽게 구할 수 있습니다.
MSE, MAE 평가 지표를 계산하기 위한 사이킷런 함수/라이브러리
mean_squared_error(y_true, y_pred): MSE 값 계산하기
mean_absolute_error(y_true, y_pred): MAE 값 계산하기
1. train_X 데이터에 대한 MSE, MAE 값을 계산하여 MSE_train, MAE_train에 저장합니다.
2. test_X 데이터에 대한 MSE, MAE 값을 계산하여 MSE_test, MAE_test에 저장합니다.
import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_squared_error
#데이터를 읽고 전 처리합니다
df = pd.read_csv("data/Advertising.csv")
df = df.drop(columns=['Unnamed: 0'])
X = df.drop(columns=['Sales'])
Y = df['Sales']
train_X, test_X, train_Y, test_Y = train_test_split(X, Y, test_size=0.2, random_state=42)
#다중 선형 회귀 모델을 초기화 하고 학습합니다
lrmodel = LinearRegression()
lrmodel.fit(train_X, train_Y)
#train_X 의 예측값을 계산합니다
pred_train = lrmodel.predict(train_X)
#1. train_X 의 MSE, MAE 값을 계산합니다
MSE_train = mean_squared_error(train_Y, pred_train)
MAE_train = mean_absolute_error(train_Y, pred_train)
print('MSE_train : %f' % MSE_train)
print('MAE_train : %f' % MAE_train)
#test_X 의 예측값을 계산합니다
pred_test = lrmodel.predict(test_X)
#2. test_X 의 MSE, MAE 값을 계산합니다
MSE_test = mean_squared_error(test_Y, pred_test)
MAE_test = mean_absolute_error(test_Y, pred_test)
print('MSE_test : %f' % MSE_test)
print('MAE_test : %f' % MAE_test)
[연습문제8] 회귀 알고리즘 평가 지표 - R2
[실습7] 에 이어서 Sales 예측 모델의 성능을 평가하기 위해서 다양한 회귀 알고리즘 평가 지표를 사용하여 비교해보겠습니다.
R2 score는 sklearn 라이브러리 함수를 통하여 쉽게 구할 수 있습니다.
R2 평가 지표를 계산하기 위한 사이킷런 함수/라이브러리
r2_score(y_true, y_pred): R2 score 값 계산하기
1. train_X 데이터에 대한 R2 값을 계산하여 R2_train에 저장합니다.
2. test_X 데이터에 대한 R2 값을 계산하여 R2_test에 저장합니다.
import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_squared_error
#데이터를 읽고 전 처리합니다
df = pd.read_csv("data/Advertising.csv")
df = df.drop(columns=['Unnamed: 0'])
X = df.drop(columns=['Sales'])
Y = df['Sales']
train_X, test_X, train_Y, test_Y = train_test_split(X, Y, test_size=0.2, random_state=42)
#다중 선형 회귀 모델을 초기화 하고 학습합니다
lrmodel = LinearRegression()
lrmodel.fit(train_X, train_Y)
#train_X 의 예측값을 계산합니다
pred_train = lrmodel.predict(train_X)
#1. train_X 의 R2 값을 계산합니다
R2_train = r2_score(train_Y, pred_train)
print('R2_train : %f' % R2_train)
#test_X 의 예측값을 계산합니다
pred_test = lrmodel.predict(test_X)
#2. test_X 의 R2 값을 계산합니다
R2_test = r2_score(test_Y, pred_test)
print('R2_test : %f' % R2_test)'개인공부 > Python' 카테고리의 다른 글
| 72. Python TreeModel 연습문제 (0) | 2021.12.07 |
|---|---|
| 71. NIPA AI온라인 교육 AI 실무 응용 과정(3) 지도학습 - 분류 (0) | 2021.12.05 |
| 69. Python Classification 연습문제 (0) | 2021.12.03 |
| 68. NIPA AI온라인 교육 AI 실무 응용 과정(1) 자료형태, 데이터 전처리 (0) | 2021.12.02 |
| 67. Python Regression 연습문제 (0) | 2021.12.01 |